Trigonometric Identities

Hie everyone..!


This is some basic information about our new unit Trigonometric Identities and to start with this unit you don't have to know all the identities off the top of your head. But these you should...

Defining relations for tangent, cotangent, secant and cosecant in terms of sine and cosine.

• The significance of an identity is that, in calculation, we may replace either 

member of the identity with the other. 

Example: Prove that -

              

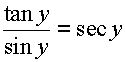
Answer-

                                     

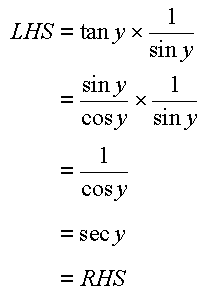
We also need to know some more identities such as Pythagorean Identities which are as follows...

Example of using Pythagorean Identities..

Prove that :

sin x cos x tan x = 1 − cos²      

 

                            Suggestions For Proving Trigonometric Identities :cises

•    Suggestions...
  1. Learn well the formulas given above of  the relations in terms of sine and cosine. The better you know the basic identities, the easier it will be to recognise what is going on in the problems.
  2. Work on the most complex side and simplify it so that it has the same form as the simplest side.
  3. Don't assume the identity to prove the identity. This means don't work on both sides of the equals side and try to meet in the middle. Start on one side and make it look like the other side.
  4. Many of these come out quite easily if you express everything on the most complex side in terms of sine and cosine only.
  5. In most examples where you see power 2 (that is, ²), it will involve using the identity sin² θ + cos² θ = 1 (or one of the other 2 formulas oh the pythagorean identity).
  Using these suggestions, you can simplify and prove expressions involving trigonometric identities.                            

                                                      

Hope this basic information will help you out in solving out problems in this lesson.

Gud Luck...:)